きる。そこで、沖側境界では入射波のスペクトルを与え、また側方境界では1つ内側の計算領域内のスペクトルと同じにするか、エネルギーが常に流出するといった条件を設定する。波向として、一π/2＜θ〈π/2の条件を与え、波は常にx軸の正方向、つまり岸方向に伝搬し、沖側方向には伝搬する成分波はないと仮定する。このように仮定することによって波のスペクトルを順次沖側から求めてゆくことができる。そのため、x軸の正方向を沖波の主方向になるべく一致させ、一π/2＜θ＜π/2の条件を越える波のエネルギーがなるべく小さくなるようにする必要がある。

2）砕波による波高減衰項の導入

砕波によって失われる波のエネルギーは個々の成分波が持っているエネルギーに比例すると仮定する。この仮定によって（1）のエネルギー平衡方程式は次のように表される。

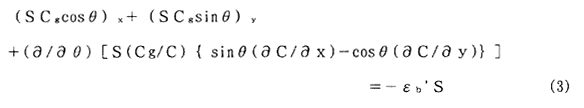
ここにεb’は単位時間内に砕波によって失われる波のエネルギーの逸散率を示す。εb'の値としては、計算格子内に進入した波が出るまでに要する平均時間に比例すると仮定して、次式で与えることにする。

さらにεbの値については、計算対象格子に入るときの砕波波高と出る時の砕波波高を、次式に示す合田の砕波指標によって求めることとした。

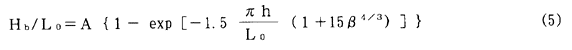
この式において、A＝0.18として求めた砕波波高以上の波はすべて砕波し、A＝0.12として求めた砕波波高以下の波高の波は砕波しないとし、砕波する波の確率がA＝0.12の波からA＝0.18の波まで線形変化すると仮定している。

前ページ　　　目次へ　　　次ページ